Inhaltsverzeichnis
Einführung
Wenn bestimmte Variablen geändert oder aktualisiert werden, werden zahlreiche Ergebnisse mithilfe einer computergestützten mathematischen Technik modelliert, die als Monte-Carlo-Simulation bekannt ist. Es handelt sich um eine Computermodellierung, mit der untersucht wird, wie komplexe Systeme funktionieren und sich verhalten. Die Methode simuliert mehrere Möglichkeiten in einem Prozess, der mit traditionellen mathematischen Methoden schwer zu lösen ist. Die Monte-Carlo-Simulation wird in vielen Bereichen eingesetzt, darunter Banken, Ingenieurwesen, Risikomanagement, Physik und Lebenszyklusanalyse (LCA).
Die Methodik basiert auf den Konzepten Zufälligkeit und Wahrscheinlichkeit. In einer Monte-Carlo-Simulation repräsentieren von einem Zufallszahlengenerator erzeugte Zufallszahlen eine bestimmte Wahrscheinlichkeitsverteilung (z. B. „Normalverteilung“). Diese Wahrscheinlichkeitsverteilung wird dann verwendet, um bestimmte Ereignisse zu bestimmen.
Die Monte-Carlo-Simulation verwendet häufig die Unsicherheitsanalyse. Die Unsicherheitsanalyse ist eine Methode zur Identifizierung von Unsicherheiten in Bezug auf Simulationsergebnisse. Die Variabilität der Simulationsergebnisse, die durch Faktoren wie Eingabezufälligkeit und modellbasierte intrinsische Variabilität verursacht wird, wird mit dieser Technik gemessen.
Die Kombination der Monte-Carlo-Simulation mit der Unsicherheitsanalyse kann ein leistungsfähiges Werkzeug sein, um das Verhalten und die Leistung eines Systems zu verstehen und zu bewerten. Um die Genauigkeit und Zuverlässigkeit von Simulationen zu verbessern, werden in diesem Artikel die Konzepte und Methoden der Monte-Carlo-Simulation und der Unsicherheitsanalyse erörtert.
Die Grundlagen der Simulation in Monte Carlo
Wahrscheinlichkeit und Zufälligkeit sind die Grundlage der Monte-Carlo-Simulation. Unter Verwendung eines Zufallszahlengenerators erzeugt der Ansatz Zufallszahlen, die dann verwendet werden, um eine bestimmte Wahrscheinlichkeitsverteilung darzustellen. Diese Wahrscheinlichkeitsverteilung wird dann verwendet, um bestimmte Ereignisse zu bestimmen.
Die vom Zufallszahlengenerator erzeugten Zufallszahlen spiegeln eine bestimmte Wahrscheinlichkeitsverteilung wieder. Diese Wahrscheinlichkeitsverteilung wird dann verwendet, um bestimmte Ereignisse zu bestimmen. Die Wahrscheinlichkeitsverteilung kann in beliebiger Form dargestellt werden, einschließlich einer Normalverteilung, Gleichverteilung oder einer Kombination aus beiden.
Dann werden die Effizienz und das Verhalten eines Systems mit Zufallszahlen nachgeahmt. Beispielsweise kann ein Finanzsystem Zufallszahlen verwenden, um den Preis einer Aktie zu replizieren. Dann werden Zufallszahlen verwendet, um verschiedene Ereignisse wie steigende oder fallende Aktienkurse zu berechnen.
Die in der Simulation verwendeten Zufallszahlen können unter Verwendung verschiedener Verfahren erzeugt werden, beispielsweise einer mathematischen Formel oder eines Zufallszahlengenerators. Mehrere Methoden können Zufallszahlen erzeugen.
Unsicherheitsanalyse
Die Unsicherheitsanalyse ist eine Methode zur Identifizierung von Unsicherheiten in Bezug auf Simulationsergebnisse. Mit dieser Technik wird die Variabilität der Simulationsergebnisse gemessen, die durch Faktoren wie Eingangszufälligkeit und modellbasierte intrinsische Variabilität verursacht wird.
Die Unsicherheitsanalyse kann auf verschiedene Arten durchgeführt werden. Eine davon ist die Sensitivitätsanalyse, die die potenziellen Auswirkungen einer Änderung der Simulationseingaben auf die Ergebnisse untersucht. Eine weitere Option ist die Durchführung einer Monte-Carlo-Simulation mit Unsicherheitsanalyse, die die Variabilität der Ergebnisse in verschiedenen Simulationen untersucht. Die Ergebnisse der Unsicherheitsanalyse können dann die Genauigkeit des Modells und die Zuverlässigkeit der Simulationsergebnisse bewerten.
Monte-Carlo-Simulation (Analyse) in der Ökobilanz – eine Fallstudie
Ein entscheidender Schritt in der Lebenszyklusanalyse (LCA) ist die Monte-Carlo-Simulation. Es kann entweder für das von uns erstellte Modell oder für einen Prozess einer Life Cycle Inventory (LCI)-Datenbank durchgeführt werden. Dies wird normalerweise für das zu modellierende System durchgeführt. Es zeigt die Ökobilanz Analytiker, wie unsicher (oder wie viel Unsicherheit) die Ergebnisse sind. Die Normalverteilung wird normalerweise verwendet, um es zu verteilen, aber es gibt auch andere Verteilungsoptionen. Die Ergebnisse werden als glockenförmige Kurve unter Verwendung der Normalverteilung angezeigt. Die Ergebnisse sind zuverlässiger, wenn die Form schmaler ist und weniger Unsicherheiten auftreten.
Excel kann zur Durchführung von Monte Carlo in verwendet werden Ökobilanz. Die einfachste Methode verwendet Ökobilanz Software wie openLCA, GaBi, oder SimaPro. Der Benutzer wird aufgefordert, die Anzahl der Läufe einzugeben, wenn die Analyse mithilfe der Software ausgeführt wird (die Anzahl der Simulationen). Typischerweise umfasst es mindestens 1000 Läufe. Die Simulationsergebnisse sind umso genauer, je höher der Lauf ist. Bei mehr als 1000 Läufen muss es jedoch viel länger dauern, bis die Analyse abgeschlossen ist. Monte Carlo funktioniert wie folgt in an Ökobilanz Software:
- Die Simulation ordnet allen zufälligen Parameterwerten Werte zwischen Minimal- und Maximalwerten zu.
- Die Software untersucht die zufälligen Parameterkonstellationen.
- Um die Analyse durchzuführen, untersuchen wir das glockenförmige Diagramm: wie sich die Unsicherheitskurve (Form) in Bezug auf die Unsicherheitsprozentsätze ändert, wenn bestimmte zufällige Parameterkombinationen verwendet werden
Japan Electricity Grid Mix
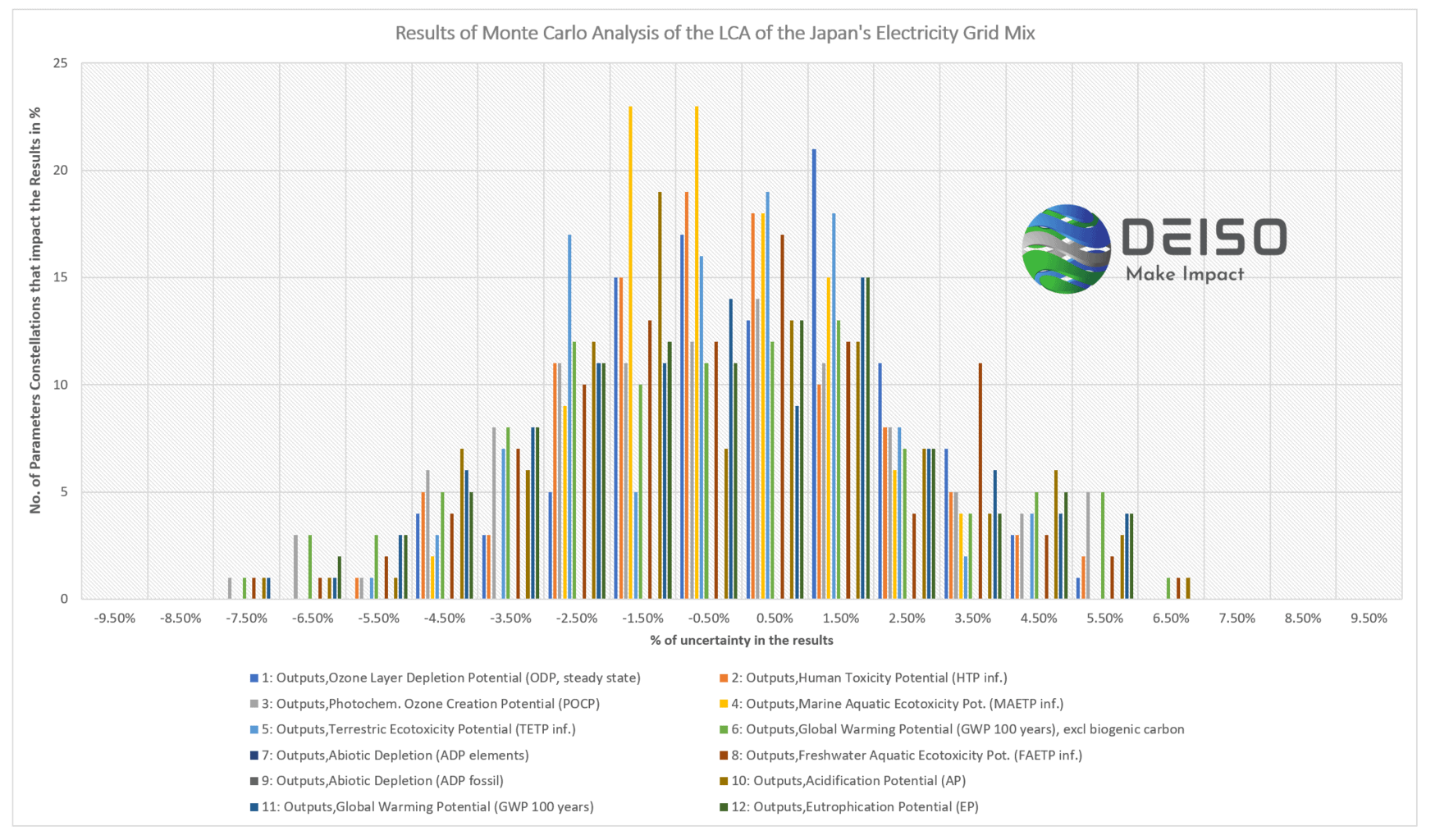
Eine Monte-Carlo-Analyse von Japans Stromnetzmix für 11 Umweltauswirkungen ist in der folgenden Abbildung dargestellt (12 Umweltauswirkungen, einschließlich des Potenzials der globalen Erwärmung mit der Ungewissheit des biogenen Kohlenstoffs, werden berücksichtigt).
Die Ergebnisse der Monte-Carlo-Analyse des japanischen Stromnetzmix
Die Y-Achse stellt „die Anzahl zufälliger Parameterkonstellationen dar, die zu Unsicherheiten für jede Wirkungskategorie (oder jedes Umweltproblem) führen. Die X-Achse repräsentiert den Prozentsatz der Unsicherheit für jede der Auswirkungskategorien. Auch hier gilt: Je schmaler die Form, desto bessere Gesamtergebnisse und robustere Ergebnisse. Je niedriger der Wert der x-Achse und je niedriger der % der y-Achse, desto besser ist das Modell in Bezug auf die Unsicherheit. Die X-Achse stellt die Nummer der Zufallsvariablen dar, in der die % der Unsicherheit auftrat, und wird auf der Y-Achse dargestellt.
Die folgende Grafik zeigt die Ungenauigkeitsanalyse für Japan Grid Mix, diesmal jedoch nur für das globale Erwärmungspotenzial (GWP) – Klimawandelpotenzial.
Sensitivitätsanalyse
Die Sensitivitätsanalyse ist eine Technik zur Bestimmung, wie sich verschiedene unabhängige Variablenwerte unter bestimmten Annahmen auf eine bestimmte abhängige Variable auswirken können. Es ist eine entscheidende Technik, die bei der Risikobewertung und Finanzanalyse verwendet wird, um herauszufinden, wie sich die Ergebnisse einer Wahl oder eines Modells ändern würden, wenn eine oder mehrere zugrunde liegende Annahmen geändert würden. Es wird auch verwendet, um zu bestimmen, welche Faktoren sich darauf auswirken, wie gut bestimmte Entscheidungen oder Modelle funktionieren, wie z. B. in der Lebenszyklusanalyse (LCA).
Die Sensitivitätsanalyse ist eine Technik zur Vorhersage, wie sich Änderungen von Faktoren wie Zinssätzen, Inflation und Wechselkursen auf die finanzielle Leistung eines Unternehmens auswirken können. Es kann auch beurteilen, wie sich verschiedene Anlagetechniken auf die erwarteten Renditen auswirken. Investoren und Management können kluge Entscheidungen treffen und ihre Risiken besser steuern, indem sie untersuchen, wie sich Änderungen bestimmter Faktoren auf die finanzielle Leistung eines Unternehmens auswirken würden.
Die Sensitivitätsanalyse wird bei der Risikobewertung und der Lebenszyklusanalyse (LCA) verwendet, um die Faktoren zu ermitteln, die sich am stärksten auf das Ergebnis eines Modells auswirken. Experten können bestimmen, welche Faktoren bei der Entscheidungsfindung und Risikokontrolle am wichtigsten sind, indem sie den Einfluss verschiedener Variablen bewerten. Mit dieser Methode werden auch die wichtigsten Annahmen für Entscheidungen und die Steuerung von Risiken ermittelt.
Finanzanalyse und Risikobewertung sind nur zwei Anwendungen der Sensitivitätsanalyse. Es kann auch untersuchen, wie sich Unternehmenstaktiken auf Marktanteile, Mitarbeitermoral und Kundenzufriedenheit auswirken. Manager und Führungskräfte können kluge Entscheidungen treffen und ihre Risiken besser managen, indem sie sich ansehen, wie sich Änderungen bestimmter Faktoren auf die Kundenzufriedenheit, das Engagement der Mitarbeiter und den Marktanteil auswirken.
Die Sensitivitätsanalyse ist entscheidend für die Risikobewertung sowie die Finanz- und Umweltanalyse. Es ist hilfreich zu wissen, welche Faktoren den größten Einfluss darauf haben, wie bestimmte Entscheidungen oder Modelle ausfallen. Es kann auch beurteilen, wie sich verschiedene Anlagestrategien auf die prognostizierten Renditen auswirken, bestimmen, welche Annahmen für die Entscheidungsfindung und das Risikomanagement am wichtigsten sind, und beurteilen, wie sich verschiedene Unternehmensstrategien auf die Kundenzufriedenheit, das Engagement der Mitarbeiter und den Marktanteil auswirken. Die Sensitivitätsanalyse ermöglicht es Anlegern und Managern, kluge Entscheidungen zu treffen und ihre Risiken besser zu managen.
Sensitivitätsanalyse in der Ökobilanz – Fallstudie
Eine weitere wesentliche Analysemethode für Ökobilanzen (LCA) ist die Sensitivitätsanalyse. Hier verwenden wir die Japan-Grid-Mix-Mote-Carlo-Analyse, um die Sensitivitätsanalyse erneut zu veranschaulichen. Die Sensitivitätsanalyse für diese Fallstudie ist in der folgenden Tabelle dargestellt. Obwohl Microsoft Excel dies auch durchführen kann, erklären wir Ihnen, wie Sie eine Sensitivitätsanalyse mit einer LCA-Software wie z. B. GaBi und das Gesamtkonzept:
- Standardabweichungen für Parameter werden mithilfe einer Sensitivitätsanalyse festgelegt.
- Die LCA-Software multipliziert und dividiert die Standardabweichung durch die Parameterwerte (z. B. +50% und -50%).
- Die Sensitivitätsanalyse zeigt, wie sich die Variation jedes Parameters auf die Ergebnisse auswirkt.
- „Wie empfindlich reagieren unsere Ergebnisse auf eine Veränderung von +/- 50% bei diesem und jenem Parameter.“
Wenn die Ergebnisse generiert werden, können Sie sich Folgendes ansehen:
- Wie viel Prozent des Ergebnisses ändert sich, wenn ein einzelner Parameter um zB 50% erhöht wird?
- Durch die Änderung nur eines Parameters änderten sich die Ergebnisse um satte, zB -50%.
Siehe die Ergebnisse der Sensitivitätsanalyse von Japans Stromnetzmix von LCA. Die erste Tabelle zeigt die Impact-Faktoren mit IDS, die den Sensitivitätsergebnissen in der zweiten Tabelle entsprechen.
1
Ozonschichtabbaupotential (ODP, stationär)
kg R11 Äquivalent
2
Humantoxizitätspotential (HTP inf.)
kg DCB-Äquivalent
3
Photochem. Ozonbildungspotential (POCP)
kg Ethen-Äq.
4
Marine Aquatic Ecotoxicity Pot. (MAETP-Inf.)
kg DCB-Äquivalent
5
Terrestrisches Ökotoxizitätspotential (TETP inf.)
kg DCB-Äquivalent
6
Treibhauspotenzial (GWP 100 Jahre), ohne biogenen Kohlenstoff
kg CO2-Äquivalent
7
Abiotischer Abbau (ADP-Elemente)
kg Sb-Äq.
8
Süßwasser Aquatic Ecotoxicity Pot. (FAETP-Inf.)
kg DCB-Äquivalent
9
Abiotischer Abbau (ADP fossil)
MJ
10
Versauerungspotential (AP)
kg SO2-Äquivalent
11
Treibhauspotenzial (GWP 100 Jahre)
kg CO2-Äquivalent
12
Eutrophierungspotential (EP)
kg Phosphat-Äq.
|
| Kohleenergie | Hydro Energie | Erdgas Energie | Kernenergie | Schweröl Energie | Solarenergie | Energie verschwenden | Windenergie |
Empfindlichkeit | 1 – Standardabweichung | -1.33% | -0.04% | -1.36% | -0.05% | -1.99% | -0.21% | 0.00% | -0.01% |
1 + Standardabweichung | 1.33% | 0.04% | 1.36% | 0.05% | 1.99% | 0.21% | 0.00% | 0.01% | |
2 – Standardabweichung | -1.58% | -0.20% | -1.05% | -0.07% | -0.78% | -0.53% | -0.22% | -0.04% | |
2 + Standardabweichung | 1.58% | 0.20% | 1.05% | 0.07% | 0.78% | 0.53% | 0.22% | 0.04% | |
3 – Standardabweichung | -2.13% | 0.00% | -1.61% | -0.01% | -0.82% | -0.01% | -0.14% | 0.00% | |
3 + Standardabweichung | 2.13% | 0.00% | 1.61% | 0.01% | 0.82% | 0.01% | 0.14% | 0.00% | |
4 – Standardabweichung | -1.53% | 0.00% | -0.22% | -0.02% | -0.12% | -0.02% | -0.54% | 0.00% | |
4 + Standardabweichung | 1.53% | 0.00% | 0.22% | 0.02% | 0.12% | 0.02% | 0.54% | 0.00% | |
5 – Standardabweichung | -1.21% | -0.02% | -1.27% | 0.00% | -0.45% | -0.05% | -1.08% | -0.06% | |
5 + Standardabweichung | 1.21% | 0.02% | 1.27% | 0.00% | 0.45% | 0.05% | 1.08% | 0.06% | |
6 – Standardabweichung | -2.29% | 0.00% | -1.84% | 0.00% | -0.68% | -0.01% | -0.17% | 0.00% | |
6 + Standardabweichung | 2.29% | 0.00% | 1.84% | 0.00% | 0.68% | 0.01% | 0.17% | 0.00% | |
7 – Standardabweichung | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
7 + Standardabweichung | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
8 – Standardabweichung | -0.80% | -0.01% | -1.62% | -0.28% | -1.91% | -0.06% | -0.05% | 0.00% | |
8 + Standardabweichung | 0.80% | 0.01% | 1.62% | 0.28% | 1.91% | 0.06% | 0.05% | 0.00% | |
9 – Standardabweichung | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
9 + Standardabweichung | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
10 – Standardabweichung | -2.35% | 0.00% | -1.18% | -0.01% | -0.90% | -0.03% | -0.23% | 0.00% | |
10 + Standardabweichung | 2.35% | 0.00% | 1.18% | 0.01% | 0.90% | 0.03% | 0.23% | 0.00% | |
11 – Standardabweichung | -2.09% | 0.00% | -1.68% | 0.00% | -0.62% | -0.01% | -0.42% | 0.00% | |
11 + Standardabweichung | 2.09% | 0.00% | 1.68% | 0.00% | 0.62% | 0.01% | 0.42% | 0.00% | |
12 – Standardabweichung | -2.13% | 0.00% | -1.48% | -0.01% | -0.76% | -0.02% | -0.27% | 0.00% | |
12 + Standardabweichung | 2.13% | 0.00% | 1.48% | 0.01% | 0.76% | 0.02% | 0.27% | 0.00% |
Fazit
Fazit 2: Der Einfluss von Zufallsvariablen und Unsicherheiten auf ein System oder einen Prozess kann mit der Monte-Carlo-Simulationsmethode untersucht werden, die oft auch als Unsicherheitsanalyse bezeichnet wird. Es ist eine Technik zur Bewertung der potenziellen Ergebnisse eines Systems oder Prozesses, indem mehrere zufällig erstellte Simulationen mit unterschiedlichen Eingabeparametern ausgeführt werden und die Ergebnisse mehrerer Simulationen zu einer Wahrscheinlichkeitsverteilung alternativer Optionen kombiniert werden. Mit dieser Technik kann das Risiko berechnet werden, das mit der Entscheidung über Investitionen angesichts der Ungewissheit verbunden ist.
Fazit 3: Die Sensitivitätsanalyse ist eine entscheidende Technik bei der Risikobewertung, der Finanzanalyse, dem Umweltmanagement und der Lebenszyklusanalyse (LCA). Es bestimmt, wie sich die Ergebnisse einer Wahl oder eines Modells ändern würden, wenn eine oder mehrere zugrunde liegende Annahmen geändert werden. Mit dieser Methode werden auch die wichtigsten Annahmen für Entscheidungen und die Steuerung von Risiken ermittelt.
Schulung zur Lebenszyklusanalyse (LCA).
Wenn Ihnen dieser Beitrag gefallen hat, abonnieren Sie unseren kostenlosen Newsletter für weitere wertvolle Inhalte! Abonnieren Sie jetzt informative Artikel, Service-Updates, herunterladbare Leitfäden und mehr. klicken Sie hier!