Tabla de contenido
Introducción
Cuando se modifican o actualizan ciertas variables, se modelan numerosos resultados utilizando una técnica matemática computarizada conocida como simulación Monte Carlo. Es un modelo informático utilizado para examinar cómo funcionan y se comportan los sistemas complejos. El método simula varias posibilidades en un proceso difícil de resolver usando métodos matemáticos tradicionales. La simulación de Monte Carlo se utiliza en muchos campos, incluidos la banca, la ingeniería, la gestión de riesgos, la física y la evaluación del ciclo de vida (LCA).
La metodología se basa en los conceptos de aleatoriedad y probabilidad. En una simulación de Monte Carlo, los números aleatorios generados por un generador de números aleatorios representan una distribución de probabilidad particular (p. ej., "distribución normal"). Esta distribución de probabilidad se usa luego para determinar ciertas ocurrencias.
La simulación de Monte Carlo a menudo utiliza análisis de incertidumbre. El análisis de incertidumbre es un método para identificar la incertidumbre en torno a los resultados de la simulación. La variabilidad en los resultados de la simulación causada por factores como la aleatoriedad de entrada y la variabilidad intrínseca basada en el modelo se mide mediante esta técnica.
La combinación de la simulación de Monte Carlo con el análisis de incertidumbre puede ser una herramienta poderosa para comprender y evaluar el comportamiento y el rendimiento de un sistema. Para mejorar la precisión y confiabilidad de las simulaciones, este artículo discutirá los conceptos y métodos de la simulación Monte Carlo y el análisis de incertidumbre.
Los fundamentos de la simulación en Monte Carlo
La probabilidad y la aleatoriedad son la base de la simulación Monte Carlo. Usando un generador de números aleatorios, el enfoque genera números aleatorios que luego se utilizan para representar una distribución de probabilidad particular. Esta distribución de probabilidad se usa luego para determinar ciertas ocurrencias.
Los números aleatorios generados por el generador de números aleatorios reflejan una distribución de probabilidad particular. Esta distribución de probabilidad se usa luego para determinar ciertas ocurrencias. La distribución de probabilidad se puede mostrar en cualquier forma, incluida una distribución normal, una distribución uniforme o una combinación de las dos.
Luego, se imita la eficiencia y el comportamiento de un sistema utilizando números aleatorios. Por ejemplo, un sistema financiero puede usar números aleatorios para replicar el precio de una acción. Luego, los números aleatorios se utilizan para calcular diferentes eventos, como el aumento o la caída de los precios de las acciones.
Los números aleatorios usados en la simulación pueden generarse usando varios métodos, como una fórmula matemática o un generador de números aleatorios. Varios métodos pueden generar números aleatorios.
Análisis de incertidumbre
El análisis de incertidumbre es un método para identificar la incertidumbre en torno a los resultados de la simulación. La variabilidad en los resultados de la simulación causada por factores como la aleatoriedad de entrada y la variabilidad intrínseca basada en el modelo se mide mediante esta técnica.
El análisis de incertidumbre puede llevarse a cabo de varias formas. Uno es el análisis de sensibilidad, que analiza los efectos potenciales de cambiar las entradas de la simulación en los resultados. Otra opción es ejecutar una simulación de Monte Carlo utilizando un análisis de incertidumbre, que analiza la variabilidad de los hallazgos en diferentes simulaciones. Los resultados del análisis de incertidumbre pueden entonces evaluar la precisión del modelo y la confiabilidad de los resultados de la simulación.
Simulación de Monte Carlo (análisis) en la evaluación del ciclo de vida: un estudio de caso
Un paso crítico en la evaluación del ciclo de vida (LCA) es la simulación de Monte Carlo. Puede llevarse a cabo para el modelo que creamos o para un proceso de una base de datos de inventario de ciclo de vida (LCI). Por lo general, se realiza para el sistema que se está modelando. muestra el ACV analista cuán inciertos (o cuánta incertidumbre) son los resultados. Normalmente se utiliza la distribución normal para distribuirlo, pero existen otras opciones de distribución. Los resultados se mostrarán como una curva en forma de campana utilizando la distribución normal. Los resultados son más confiables cuando la forma es más estrecha y cuando hay menos ocurrencias de incertidumbres.
Excel se puede utilizar para realizar Monte Carlo en ACV. El método más simple utiliza ACV software como abiertoLCA, GaBi, o SimaPro. Se le pedirá al usuario que ingrese el número de ejecuciones cuando ejecute el análisis usando el software (el número de simulaciones). Por lo general, implica al menos 1000 ejecuciones. Los resultados de la simulación son más precisos cuanto mayor sea la ejecución. Aún así, el tiempo debe llevar mucho más tiempo para completar el análisis si hay más de 1000 ejecuciones. Monte Carlo opera de la siguiente manera en un ACV software:
- La simulación asigna todos los valores de parámetros aleatorios entre valores mínimos y máximos.
- El software examina las constelaciones de parámetros aleatorios.
- Para realizar el análisis, examinamos el gráfico en forma de campana: cómo cambia la curva de incertidumbre (forma) en términos de porcentajes de incertidumbre cuando se usan ciertas combinaciones de parámetros aleatorios
Mezcla de red eléctrica de Japón
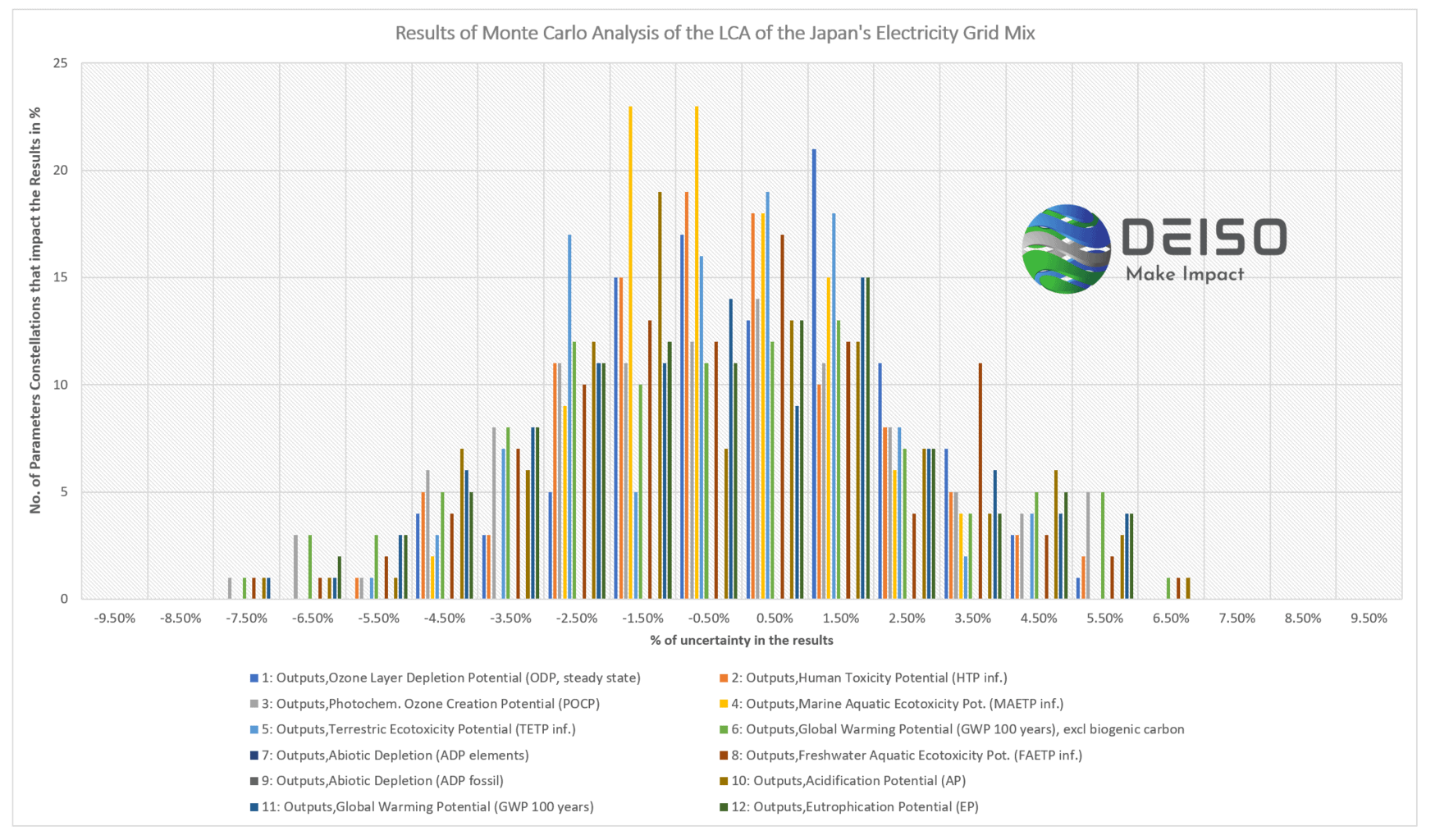
En la siguiente figura se muestra un análisis de Monte Carlo de la combinación de la red eléctrica de Japón para 11 impactos ambientales (se consideran 12 impactos ambientales, incluido el potencial de calentamiento global con incertidumbre de carbono biogénico).
Los resultados del análisis de Monte Carlo de la combinación de la red eléctrica de Japón
El eje Y representa “el número de constelaciones de parámetros aleatorios que generan incertidumbre para cada categoría de impacto (o problema ambiental). El eje X representa el porcentaje de incertidumbre para cada una de las categorías de impacto. Una vez más, cuanto más estrecha sea la forma, mejores serán los resultados generales y más sólidos. Además, cuanto menor sea el valor del eje x y menor sea el % del eje Y, mejor modelo en términos de incertidumbre. El eje X representa el número de la variable aleatoria en la que se produjo el % de incertidumbre y se representa en el eje Y.
El siguiente gráfico muestra un análisis de falta de veracidad para Japan Grid Mix, pero esta vez solo para el potencial de calentamiento global (GWP): potencial de cambio climático.
Análisis de sensibilidad
El análisis de sensibilidad es una técnica para determinar cómo varios valores de variables independientes pueden afectar una variable dependiente particular bajo un conjunto específico de suposiciones. Es una técnica crucial utilizada en la evaluación de riesgos y el análisis financiero que ayuda a determinar cómo variarían los resultados de una elección o modelo si se cambiaran uno o más supuestos subyacentes. También se usa para determinar qué factores afectan qué tan bien funcionan las opciones o modelos específicos, como en la Evaluación del ciclo de vida (LCA).
El análisis de sensibilidad es una técnica para predecir cómo los cambios en factores como las tasas de interés, la inflación y los tipos de cambio pueden afectar el desempeño financiero de una empresa. También puede evaluar cómo diversas técnicas de inversión afectan los rendimientos previstos. Los inversionistas y la administración pueden hacer juicios acertados y administrar mejor sus riesgos al examinar cómo los cambios en ciertos factores afectarían el desempeño financiero de una empresa.
El análisis de sensibilidad se utiliza en la evaluación de riesgos y la evaluación del ciclo de vida (LCA) para identificar los factores que más afectan el resultado de un modelo. Los expertos pueden determinar qué factores son más cruciales al tomar decisiones y controlar los riesgos al evaluar la influencia de varias variables. Los supuestos más cruciales para tomar decisiones y controlar los riesgos también se determinan utilizando este método.
El análisis financiero y la evaluación de riesgos son solo dos aplicaciones del análisis de sensibilidad. También puede examinar cómo las tácticas corporativas afectan la participación de mercado, la moral del personal y la satisfacción del cliente. Los gerentes y ejecutivos pueden tomar decisiones acertadas y administrar mejor sus riesgos observando cómo los cambios en ciertos factores afectarán la felicidad del cliente, el compromiso del personal y la participación de mercado.
El análisis de sensibilidad es crucial para la evaluación de riesgos y el análisis financiero y ambiental. Es útil saber qué factores tienen el mayor impacto en el resultado de opciones o modelos específicos. También puede evaluar cómo diversas estrategias de inversión afectan los rendimientos proyectados, determinar qué presunciones son más cruciales para la toma de decisiones y la gestión de riesgos, y evaluar cómo diversas estrategias de la empresa afectan la satisfacción del cliente, el compromiso del personal y la participación en el mercado. El análisis de sensibilidad permite a los inversores y gestores tomar decisiones acertadas y gestionar mejor sus riesgos.
Análisis de sensibilidad en la evaluación del ciclo de vida: estudio de caso
Otro método de análisis esencial para la evaluación del ciclo de vida (LCA) es el análisis de sensibilidad. Aquí, usamos el análisis Japan Grid Mix Mote Carlo para ilustrar nuevamente el análisis de sensibilidad. El análisis de sensibilidad para este estudio de caso se muestra en la siguiente tabla. Aunque Microsoft Excel también puede realizarlo, explicaremos cómo realizar un análisis de sensibilidad con un software LCA como, por ejemplo, GaBi y el concepto general:
- Las desviaciones estándar de los parámetros se establecerán mediante análisis de sensibilidad.
- El software LCA multiplica y divide la desviación estándar por los valores de los parámetros (por ejemplo, +50% y -50%).
- El análisis de sensibilidad demuestra cómo la variación de cada parámetro afecta los resultados.
- “Cuán sensibles son nuestros resultados a un cambio de +/- 50% en este y aquel parámetro”.
Cuando se generan los resultados, puede ver lo siguiente:
- ¿Qué porcentaje del resultado cambió si un solo parámetro se incrementó, por ejemplo, 50%?
- Al cambiar solo un parámetro, los resultados cambiaron muchísimo, por ejemplo, -50%.
Vea los resultados del análisis de sensibilidad de la combinación de LCA de la red eléctrica de Japón. La primera tabla muestra los factores de impacto dentro del IDS correspondientes a los resultados de sensibilidad de la segunda tabla.
1
Potencial de agotamiento de la capa de ozono (ODP, estado estacionario)
kg R11 equiv.
2
Potencial de toxicidad humana (HTP inf.)
kg DCB eq.
3
fotoquímica Potencial de creación de ozono (POCP)
kg Eteno eq.
4
Olla de Ecotoxicidad Acuática Marina. (Inf. MAETP)
kg DCB eq.
5
Potencial de Ecotoxicidad Terrestre (TETP inf.)
kg DCB eq.
6
Potencial de Calentamiento Global (GWP 100 años), excluyendo carbono biogénico
kg CO2 eq.
7
Agotamiento abiótico (elementos ADP)
kg Sb eq.
8
Olla de ecotoxicidad acuática de agua dulce. (Inf. FAETP)
kg DCB eq.
9
Agotamiento abiótico (fósil ADP)
M.J.
10
Potencial de Acidificación (AP)
kg SO2 eq.
11
Potencial de calentamiento global (GWP 100 años)
kg CO2 eq.
12
Potencial de eutrofización (EP)
kg Fosfato eq.
|
| Energía del carbón | Energía hidro | Energía de gas natural | Energía nuclear | Energía de fuelóleo pesado | Energía solar | Gastar energía | Energía eólica |
Sensibilidad | 1 – Desviación estándar | -1.33% | -0.04% | -1.36% | -0.05% | -1.99% | -0.21% | 0.00% | -0.01% |
1 + desviación estándar | 1.33% | 0.04% | 1.36% | 0.05% | 1.99% | 0.21% | 0.00% | 0.01% | |
2 – Desviación estándar | -1.58% | -0.20% | -1.05% | -0.07% | -0.78% | -0.53% | -0.22% | -0.04% | |
2 + desviación estándar | 1.58% | 0.20% | 1.05% | 0.07% | 0.78% | 0.53% | 0.22% | 0.04% | |
3 – Desviación estándar | -2.13% | 0.00% | -1.61% | -0.01% | -0.82% | -0.01% | -0.14% | 0.00% | |
3 + desviación estándar | 2.13% | 0.00% | 1.61% | 0.01% | 0.82% | 0.01% | 0.14% | 0.00% | |
4 – Desviación estándar | -1.53% | 0.00% | -0.22% | -0.02% | -0.12% | -0.02% | -0.54% | 0.00% | |
4 + desviación estándar | 1.53% | 0.00% | 0.22% | 0.02% | 0.12% | 0.02% | 0.54% | 0.00% | |
5 – Desviación estándar | -1.21% | -0.02% | -1.27% | 0.00% | -0.45% | -0.05% | -1.08% | -0.06% | |
5 + desviación estándar | 1.21% | 0.02% | 1.27% | 0.00% | 0.45% | 0.05% | 1.08% | 0.06% | |
6 – Desviación estándar | -2.29% | 0.00% | -1.84% | 0.00% | -0.68% | -0.01% | -0.17% | 0.00% | |
6 + desviación estándar | 2.29% | 0.00% | 1.84% | 0.00% | 0.68% | 0.01% | 0.17% | 0.00% | |
7 – Desviación estándar | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
7 + desviación estándar | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
8 – Desviación estándar | -0.80% | -0.01% | -1.62% | -0.28% | -1.91% | -0.06% | -0.05% | 0.00% | |
8 + desviación estándar | 0.80% | 0.01% | 1.62% | 0.28% | 1.91% | 0.06% | 0.05% | 0.00% | |
9 – Desviación estándar | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
9 + desviación estándar | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
10 – Desviación estándar | -2.35% | 0.00% | -1.18% | -0.01% | -0.90% | -0.03% | -0.23% | 0.00% | |
10 + desviación estándar | 2.35% | 0.00% | 1.18% | 0.01% | 0.90% | 0.03% | 0.23% | 0.00% | |
11 – Desviación estándar | -2.09% | 0.00% | -1.68% | 0.00% | -0.62% | -0.01% | -0.42% | 0.00% | |
11 + desviación estándar | 2.09% | 0.00% | 1.68% | 0.00% | 0.62% | 0.01% | 0.42% | 0.00% | |
12 – Desviación estándar | -2.13% | 0.00% | -1.48% | -0.01% | -0.76% | -0.02% | -0.27% | 0.00% | |
12 + desviación estándar | 2.13% | 0.00% | 1.48% | 0.01% | 0.76% | 0.02% | 0.27% | 0.00% |
Conclusión
Conclusión 2: La influencia de las variables aleatorias y las incertidumbres en un sistema o proceso puede estudiarse utilizando el método de simulación de Monte Carlo, también conocido como análisis de incertidumbre. Es una técnica para evaluar los resultados potenciales de un sistema o proceso mediante la ejecución de varias simulaciones creadas aleatoriamente y con diferentes parámetros de entrada y la combinación de los resultados de varias simulaciones da como resultado una distribución de probabilidad de opciones alternativas. El riesgo asociado a decidir sobre inversiones ante la incertidumbre puede calcularse utilizando esta técnica.
Conclusión 3: El análisis de sensibilidad es una técnica crucial en la evaluación de riesgos, el análisis financiero, la gestión ambiental y la evaluación del ciclo de vida (LCA). Determina cómo variarían los resultados de una elección o modelo si se cambiaran uno o más supuestos subyacentes. Los supuestos más cruciales para tomar decisiones y controlar los riesgos también se determinan utilizando este método.
Capacitación sobre evaluación del ciclo de vida (LCA)
Si te ha gustado esta publicación, únete a nuestro boletín gratuito para obtener más contenido valioso. Suscríbase ahora para recibir artículos informativos, actualizaciones de servicios, guías descargables y más. haga clic aquí!