Introduction
When certain variables are changed or updated, numerous outcomes are modeled using a computerized mathematical technique known as Monte Carlo simulation. It is a computer modeling used to examine how complex systems operate and behave. The method simulates several possibilities in a process challenging to solve using traditional mathematical methods. Monte Carlo simulation is used in many fields, including banking, engineering, risk management, physics, and Life Cycle Assessment (LCA).
The methodology is founded on the concepts of randomness and probability. In a Monte Carlo simulation, random numbers generated by a random number generator represent a particular probability distribution (e.g., “normal distribution). This probability distribution is then used to determine certain occurrences.
Monte Carlo simulation often uses uncertainty analysis. Uncertainty analysis is a method for identifying uncertainty around simulation results. The variability in simulation results caused by factors like input randomness and model-based intrinsic variability is measured using this technique.
Combining Monte Carlo simulation with uncertainty analysis may be a powerful tool for understanding and evaluating the behavior and performance of a system. To improve the accuracy and reliability of simulations, this article will discuss the concepts and methods of Monte Carlo simulation and uncertainty analysis.
The Basics of Simulation in Monte Carlo
Probability and randomness are the basis of Monte Carlo simulation. Using a random number generator, the approach generates random numbers that are then utilized to represent a particular probability distribution. This probability distribution is then used to determine certain occurrences.
The random numbers generated by the random number generator reflect a particular probability distribution. This probability distribution is then used to determine certain occurrences. The probability distribution may be shown in any shape, including a normal distribution, uniform distribution, or a combination of the two.
Then, a system’s efficiency and behavior are imitated using random numbers. For instance, a financial system may use random numbers to replicate the price of a stock. Then, random numbers are used to calculate different events, such as rising or falling stock prices.
The random numbers used in the simulation may be generated using various methods, such as a mathematical formula or a random number generator. Several methods may generate random numbers.
Uncertainty Analysis
Uncertainty analysis is a method for identifying uncertainty around simulation results. The variability in simulation results caused by factors like input randomness and model-based intrinsic variability is measured using this technique.
Uncertainty analysis may be carried out in several ways. One is sensitivity analysis, which looks at the potential effects of changing the simulation’s inputs on the outcomes. Another option is to run a Monte Carlo simulation using uncertainty analysis, which looks at the findings’ variability across different simulations. The uncertainty analysis results may then assess the accuracy of the model and the dependability of the simulation results.
Monte Carlo Simulation (Analysis) in Life Cycle Assessment - A Case Study
A critical step in Life Cycle Assessment (LCA) is the Monte Carlo simulation. It can be carried out for either the model we create or a process of a Life Cycle Inventory (LCI) database. It is typically done for the system that is being modeled. It shows the LCA analyst how uncertain (or how much uncertainty) the results are. The normal distribution is typically used to distribute it, but other distribution options exist. The results will be displayed as a bell-shaped curve using the normal distribution. The results are more reliable when the shape is narrower and when there are fewer occurrences of uncertainties.
Excel can be used to carry out Monte Carlo in LCA. The simplest method uses LCA software like openLCA, GaBi, or SimaPro. The user will be prompted to enter the number of runs when running the analysis using software (the number of simulations). Typically, it involves at least 1000 runs. The simulation results are more accurate the higher the run. Still, time must take much longer to complete the analysis if more than 1000 runs. Monte Carlo operates as follows in an LCA software:
- The simulation assigns all random parameter values between minimum and maximum values.
- The software examines the random parameter constellations.
- To conduct the analysis, we examine the bell-shaped graph: how the uncertainty curve (shape) changes in terms of uncertainty percentages when certain random parameter combinations are used
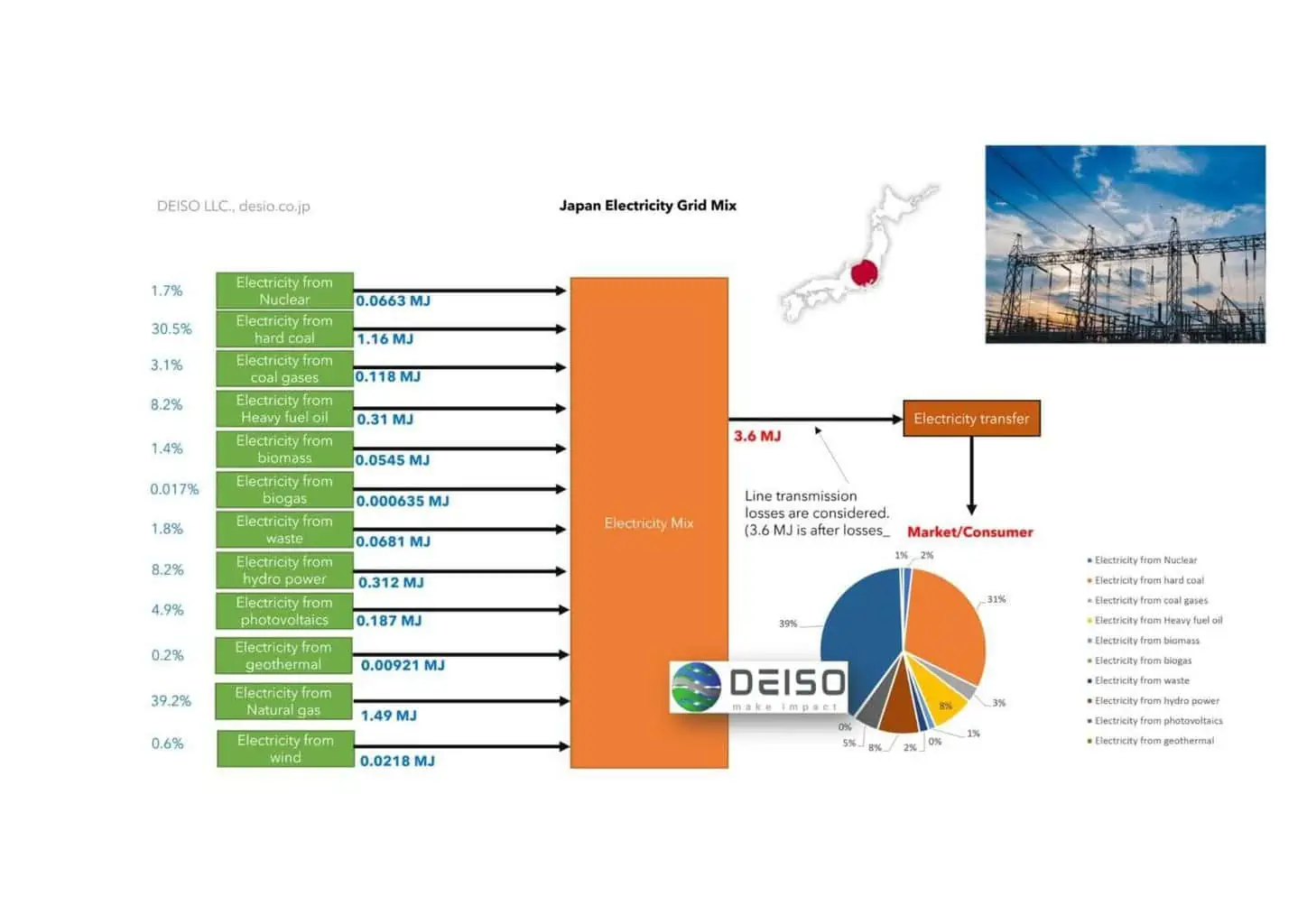
Japan Electricity Grid Mix
A Monte Carlo analysis of Japan’s electricity grid mix for 11 environmental impacts is shown in the following figure (12 environmental impacts, including Global Warming potential with biogenic carbon uncertainty, are considered).
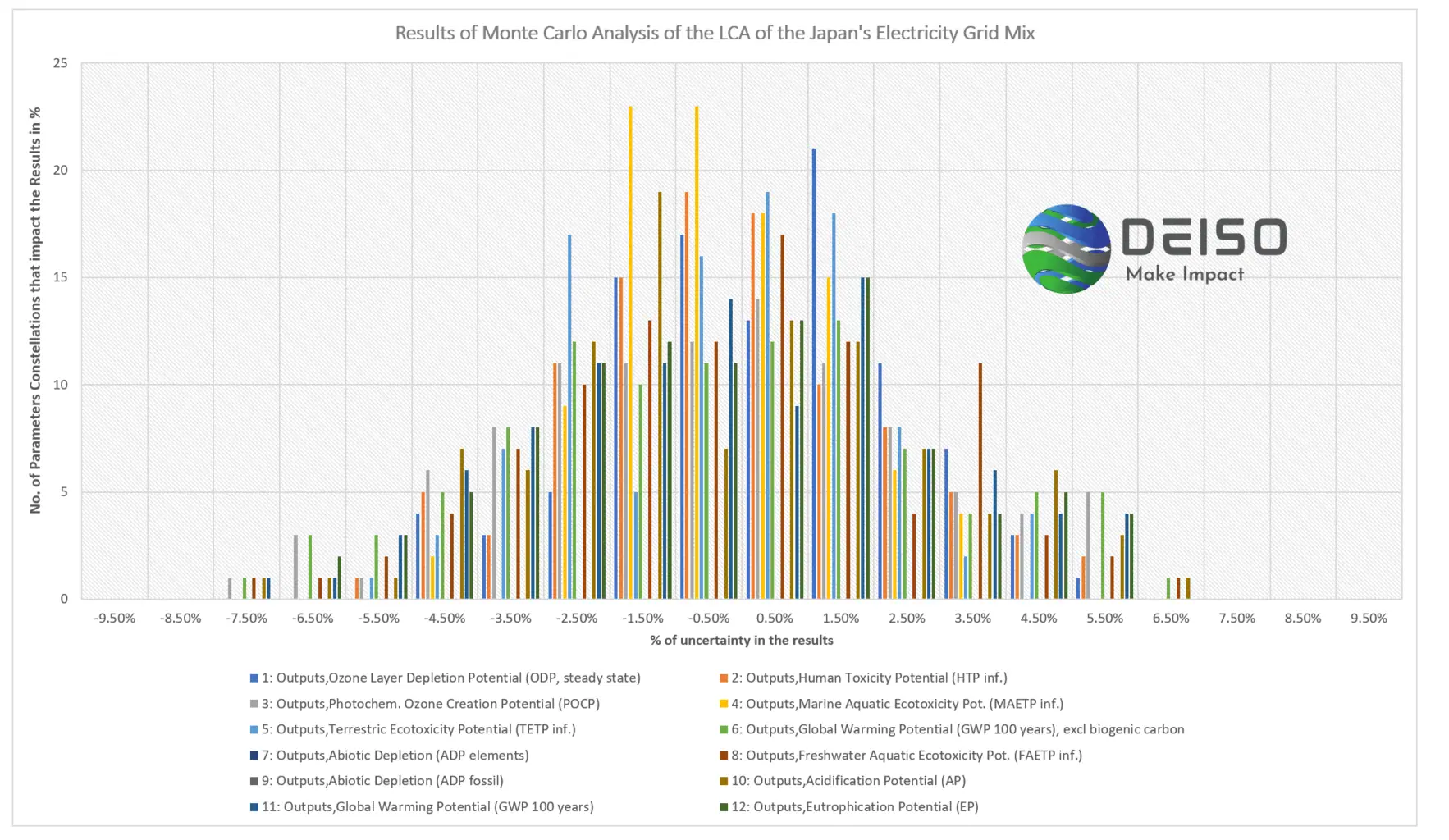
The Results of the Monte Carlo Analysis of the Japan Electricity Grid Mix
The Y-Axis represents “the number of random parameters constellations that lead to uncertainty for each impact category (or environmental issue). The X-Axis represents the percentage of uncertainty for each of the impact categories. Again, the narrow the shape, the better overall and more robust results. Also, the lower the value of the x-axis and the lower the % of the Y-axis, the better model in terms of uncertainty. The X-Axis represents the number of the random variable in which the % of uncertainty occurred and is represented in the Y-axis.
The following graph shows unveracity analysis for Japan Grid Mix but this time for Global Warming Potential (GWP) only – Climate Change Potential.
Sensitivity Analysis
Sensitivity analysis is a technique for determining how various independent variable values may impact a particular dependent variable under a specific set of assumptions. It is a crucial technique used in risk assessment and financial analysis that aids in figuring out how the outcomes of a choice or model would vary if one or more underlying assumptions were changed. It’s also used to determine which factors impact how well specific choices or models work, like in Life Cycle Assessment (LCA).
Sensitivity analysis is a technique to predict how changes in factors like interest rates, inflation, and exchange rates may impact a company’s financial performance. It may also assess how various investing techniques affect anticipated returns. Investors and management may make wise judgments and better manage their risks by examining how changes in certain factors would impact a company’s financial performance.
Sensitivity analysis is used in risk assessment and Life Cycle Assessment (LCA) to pinpoint the factors that most impact a model’s result. Experts can determine which factors are most crucial when making choices and controlling risks by assessing the influence of various variables. The most crucial assumptions for making choices and controlling risks are also determined using this method.
Financial analysis and risk assessment are just two applications of sensitivity analysis. It may also examine how corporate tactics affect market share, staff morale, and customer satisfaction. Managers and executives may make wise choices and better manage their risks by looking at how changes in certain factors will impact customer happiness, staff engagement, and market share.
Sensitivity analysis is crucial for risk assessment and financial and environmental analysis. It is helpful to know which factors have the most impact on how specific choices or models turn out. It may also assess how various investment strategies affect projected returns, determine which presumptions are most crucial for decision-making and risk management, and assess how various company strategies affect client satisfaction, staff engagement, and market share. Sensitivity analysis allows investors and managers to make wise choices and better manage their risks.
Sensitivity Analysis in Life Cycle Assessment – Case Study
Another essential analysis method for Life Cycle Assessment (LCA) is sensitivity analysis. Here, we use the Japan Grid Mix Mote Carlo analysis to illustrate sensitivity analysis again. The sensitivity analysis for this case study is shown in the table below. Although Microsoft Excel can also perform it, we will explain how to perform sensitivity analysis with an LCA software like, e.g., GaBi and the overall concept:
- Standard deviations for parameters will be set using sensitivity analysis.
- The LCA software multiplies and divides the standard deviation by the parameter values (for example, +50% and -50%).
- The sensitivity analysis demonstrates how each parameter’s variation affects the outcomes.
- “How sensitive are our results to a +/- 50% change in this and that parameter.”
When the results are generated, you can look at the following:
- What percentage of the result changed if a single parameter was increased by, e.g., 50%?
- By changing just one parameter, the results changed by a whopping, e.g., -50%.
See the results of the sensitivity analysis of Japan’s electricity grid mix of LCA. The first table shows the impact factors withier IDS corresponding to the sensitivity results in the second table.
1
Ozone Layer Depletion Potential (ODP, steady state)
kg R11 eq.
2
Human Toxicity Potential (HTP inf.)
kg DCB eq.
3
Photochem. Ozone Creation Potential (POCP)
kg Ethene eq.
4
Marine Aquatic Ecotoxicity Pot. (MAETP inf.)
kg DCB eq.
5
Terrestric Ecotoxicity Potential (TETP inf.)
kg DCB eq.
6
Global Warming Potential (GWP 100 years), excl biogenic carbon
kg CO2 eq.
7
Abiotic Depletion (ADP elements)
kg Sb eq.
8
Freshwater Aquatic Ecotoxicity Pot. (FAETP inf.)
kg DCB eq.
9
Abiotic Depletion (ADP fossil)
MJ
10
Acidification Potential (AP)
kg SO2 eq.
11
Global Warming Potential (GWP 100 years)
kg CO2 eq.
12
Eutrophication Potential (EP)
kg Phosphate eq.
|
| Coal Energy | Hydro Energy | NaturalGas Energy | Nuclear Energy | Heavy Fuel Oil Energy | Solar Energy | Waste Energy | Wind Energy |
Sensitivity | 1 – Standard deviation | -1.33% | -0.04% | -1.36% | -0.05% | -1.99% | -0.21% | 0.00% | -0.01% |
1 + Standard deviation | 1.33% | 0.04% | 1.36% | 0.05% | 1.99% | 0.21% | 0.00% | 0.01% | |
2 – Standard deviation | -1.58% | -0.20% | -1.05% | -0.07% | -0.78% | -0.53% | -0.22% | -0.04% | |
2 + Standard deviation | 1.58% | 0.20% | 1.05% | 0.07% | 0.78% | 0.53% | 0.22% | 0.04% | |
3 – Standard deviation | -2.13% | 0.00% | -1.61% | -0.01% | -0.82% | -0.01% | -0.14% | 0.00% | |
3 + Standard deviation | 2.13% | 0.00% | 1.61% | 0.01% | 0.82% | 0.01% | 0.14% | 0.00% | |
4 – Standard deviation | -1.53% | 0.00% | -0.22% | -0.02% | -0.12% | -0.02% | -0.54% | 0.00% | |
4 + Standard deviation | 1.53% | 0.00% | 0.22% | 0.02% | 0.12% | 0.02% | 0.54% | 0.00% | |
5 – Standard deviation | -1.21% | -0.02% | -1.27% | 0.00% | -0.45% | -0.05% | -1.08% | -0.06% | |
5 + Standard deviation | 1.21% | 0.02% | 1.27% | 0.00% | 0.45% | 0.05% | 1.08% | 0.06% | |
6 – Standard deviation | -2.29% | 0.00% | -1.84% | 0.00% | -0.68% | -0.01% | -0.17% | 0.00% | |
6 + Standard deviation | 2.29% | 0.00% | 1.84% | 0.00% | 0.68% | 0.01% | 0.17% | 0.00% | |
7 – Standard deviation | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
7 + Standard deviation | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
8 – Standard deviation | -0.80% | -0.01% | -1.62% | -0.28% | -1.91% | -0.06% | -0.05% | 0.00% | |
8 + Standard deviation | 0.80% | 0.01% | 1.62% | 0.28% | 1.91% | 0.06% | 0.05% | 0.00% | |
9 – Standard deviation | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
9 + Standard deviation | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
10 – Standard deviation | -2.35% | 0.00% | -1.18% | -0.01% | -0.90% | -0.03% | -0.23% | 0.00% | |
10 + Standard deviation | 2.35% | 0.00% | 1.18% | 0.01% | 0.90% | 0.03% | 0.23% | 0.00% | |
11 – Standard deviation | -2.09% | 0.00% | -1.68% | 0.00% | -0.62% | -0.01% | -0.42% | 0.00% | |
11 + Standard deviation | 2.09% | 0.00% | 1.68% | 0.00% | 0.62% | 0.01% | 0.42% | 0.00% | |
12 – Standard deviation | -2.13% | 0.00% | -1.48% | -0.01% | -0.76% | -0.02% | -0.27% | 0.00% | |
12 + Standard deviation | 2.13% | 0.00% | 1.48% | 0.01% | 0.76% | 0.02% | 0.27% | 0.00% |
Conclusion
Conclusion 2: The influence of random variables and uncertainties on a system or process may be studied using the Monte Carlo simulation method, also often known as uncertainty analysis. It is a technique for evaluating the potential outcomes of a system or process by running several simulations created randomly and having different input parameters and combining the results of several simulations results in a probability distribution of alternative options. The risk associated with deciding on investments in the face of uncertainty may be calculated using this technique.
Conclusion 3: Sensitivity analysis is a crucial technique in risk assessment, financial analysis, environmental management, and Life Cycle Assessment (LCA). It determines how the outcomes of a choice or model would vary if one or more underlying assumptions are changed. The most crucial assumptions for making choices and controlling risks are also determined using this method.
